- Details
-
Published: Wednesday, November 20 2024 01:00
Decades of quantum research are now being transformed into practical technologies, including the superconducting circuits that are being used in physics research and built into small quantum computers by companies like IBM and Google. The established knowledge and technical infrastructure are allowing researchers to harness quantum technologies in unexpected, innovative ways and creating new research opportunities.
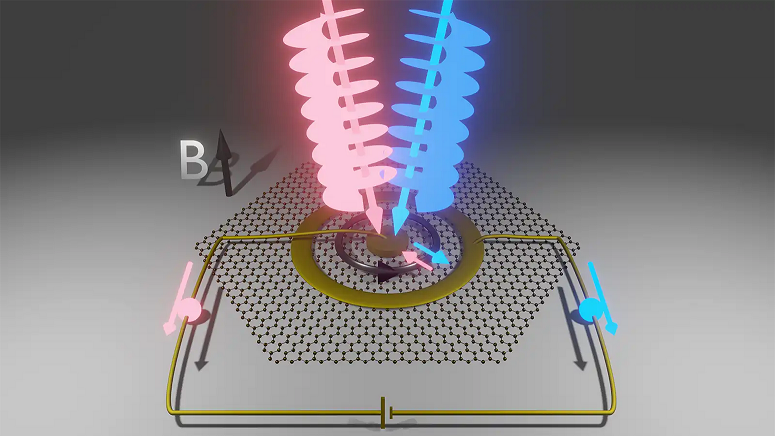
For superconducting circuits to be used as qubits—the basic building blocks of a quantum computer—the circuits need to reliably interact with delicate quantum states while keeping them carefully isolated from other influences. Superconducting circuits and the quantum states that occur in them are both sensitive to external influences, like shifting temperatures, stray electric fields or a passing particle, so manipulating qubits without external disruption is a delicate art.  Instead of fashioning qubits in their superconducting circuits, researchers incorporated a sample with a magnetic layer atop a superconductor. They were able to use the sensitivity of the circuit to explore the quantum world hidden in the sample. The above image shows the changes in the circuit’s behavior as an applied magnetic field and the circuit’s properties were varied, revealing a strong interaction between the superconducting and ferromagnetic properties of the sample. (Credit: Harvard University)
Instead of fashioning qubits in their superconducting circuits, researchers incorporated a sample with a magnetic layer atop a superconductor. They were able to use the sensitivity of the circuit to explore the quantum world hidden in the sample. The above image shows the changes in the circuit’s behavior as an applied magnetic field and the circuit’s properties were varied, revealing a strong interaction between the superconducting and ferromagnetic properties of the sample. (Credit: Harvard University)
The sensitivity of superconducting circuits means that minor blemishes in fabrication and installation can ruin a qubit, so much work has gone into establishing precise fabrication techniques to produce usable tech. All that work now means that the underlying sensitivity that makes superconducting qubits a pain to work with can be exploited as part of a quantum sensor.
In a paper published in the journal Nature Physics earlier this year, a collaboration between theorists at JQI and experimentalists at Harvard University presented a technique that repurposes the technology of superconducting circuits to study samples with exotic forms of superconductivity. The collaboration demonstrated that by building samples of interest into a superconducting circuit they could spy on exotic superconducting behaviors that have eluded existing measurement techniques.
“Essentially, we turned bugs of superconducting qubits into features,” says JQI postdoctoral researcher Andrey Grankin, who is an author of the paper.
The team’s experiments provided a new way to distinguish exotic forms of superconductivity from the conventional, well-understood variety. The technique also allowed them to study superconducting currents that occur in such a thin section of a sample that most existing techniques for researching superconductivity aren’t reliable. Their results also suggest that the approach might be beneficial in other areas of condensed matter research—the field that studies how the interactions of the multitude of particles in a material produce its properties.
“By capitalizing on this technology from the quantum computing side of things, it turns out that we were able to show that this is actually a very nice sensor for looking at fundamental condensed matter physics problems, in particular for understanding superconductivity in very small systems,” says Harvard physics graduate student Nick Poniatowski, who is a co-lead author of the paper.
Superconducting circuits commonly rely on resonators in which electromagnetic waves bounce around for extended periods and interact with quantum states. Researchers can use the bouncing waves to both manipulate a nearby qubit and determine what state it is in.
The project started when researchers at Harvard began experimenting with placing a sample near the resonator instead of building a qubit there. Incorporating a sample into the superconducting circuits provided the researchers with a convenient way to send currents through the sample as well as a built-in sensor, in the form of the resonator, to detect subtle changes in its electronic states.
In particular, the team studied samples where a magnetic layer lies on a superconductor, which research indicated might be a promising environment for hunting down exotic forms of superconductivity.
Ordinary superconductivity doesn’t mix well with magnetism, but researchers have discovered signs of interesting interactions that occur when magnetic and superconducting materials are brought together. Superconductivity and magnetism are connected because electrons must be paired up to create a superconducting current and magnetism influences how electrons can partner up.
Every electron has a quantum property called spin, which makes it behave similarly to a tiny magnet. Like a bar magnet will flip around when it is forced toward a magnet with the same orientation, electrons want the magnetic fields of their spins to point in opposite directions. As a result, the best-understood superconductors have electrons that pair with counterparts with the opposite spin. But magnetic materials—ferromagnets—have a magnetic field that works to twist all the electrons so that their fields point the same way, preventing such pairings.
However, experiments have indicated that there are likely more exotic forms of superconductivity with alternative ways that electrons form pairs. Some of the exotic pairings—called spin-triplet pairings—have spins that point in the same direction. Evidence suggests that spin-triplet pairs might be found in certain seemingly conventional superconductors, just in small numbers that are obscured by the large crowd of traditional superconducting pairs.
Prior results have indicated that at the interface of a ferromagnet and a superconductor, some spin-triplet electron pairs from the superconductor might be able to bleed over into the magnetic territory. Researchers hope that studying exotic superconductors and their pairing mechanisms will open new opportunities in research and quantum computing and possibly even identify a superconductor that works under more convenient conditions than the frigid temperatures or high pressures required for known superconductors.
In the new work, the experimentalists chose samples composed of a magnetic layer of a material called permalloy attached to a superconducting layer of niobium. As they performed experiments, they weren’t getting a clear picture of what was happening at the interface or identifying a smoking gun to indicate unconventional superconductivity, so they turned to theorists. Poniatowski previously studied physics as an undergraduate at UMD, and he knew that Grankin and Professor and JQI Fellow Victor Galitski had an interest in the theories that describe superconducting qubits. Poniatowski reached out, and Grankin and Galitski, who is also a Chesapeake Chair Professor of Theoretical Physics in the Department of Physics, joined the project.
“Eventually, Andrey came up with these models that then guided us a little bit more in the experiment to perform certain experimental tests,” says Yale postdoctoral associate Charlotte Bøttcher, a co-lead author of the paper who was a Harvard graduate student when she performed this research. “Before that, it was like shooting a little bit in the dark and just trying to play with whatever we had available. But then the interaction with theory was really what made things come together.”
The experiment needed a clear way of distinguishing exotic electron pairs from their conventional counterparts. Normally, measuring the electrical resistance—a material’s opposition to currents, which make electric circuits lose energy—is a cornerstone of superconductor research since the defining feature of a superconducting current is that it experiences no resistance. But all superconductors having zero resistance means resistance measurements can’t distinguish between exotic and traditional superconducting paired electrons.
However, a superconductor can have a distinctive inductance—a material’s resistance to changes in the electrical current. The inductance depends on many things, like the size and shape of the material. In superconductors, the inductance depends on the number of superconducting electron pairs that are present, with the dependence getting more dramatic the fewer electron pairs there are. The team focused on measuring the inductance to tease out what was occurring near the interface.
“Really, the advantage of our probe is we're measuring the badness of the superconductor not the goodness,” says Poniatowski. “So if a superconducting current is very weak, we can see a very strong response.”
Using this technique allowed the team not only to measure how much superconductivity occurred at the interfaces but also to observe how that amount changed as they varied the temperature. This was crucial to distinguishing what type of superconductivity they were observing. Since the exotic spin-triplet pairs are more delicate than their traditional counterparts, their population should fall off much more quickly as the temperature increases.
The team obtained even more information by performing the experiments with the sample placed in magnetic fields that pointed in various directions relative to the flow of the electrical current. Grankin’s contributions included determining how the experimental signatures should differ if the magnetic field points along the direction of the current or perpendicular to it.
The population changes they observed matched the signature of the exotic spin-triplet states described by the theory.
“Using this new technique borrowing from quantum information technologies we were able to actually see evidence for this very subtle, hard-to-detect exotic pairing state in this simple system,” says Poniatowski.
While the results indicated the presence of exotic superconductivity, they also revealed further mysteries to be investigated about how those states can exist in the material. The theories predict that in addition to being disrupted easily by heat, the superconducting states should also be easily disrupted by any mess in the material’s structure.
“Typically, this state is so fragile that any disorder should kill the state,” says Bøttcher. “And our systems are, for sure, not perfect, so it's a bit of a puzzle why this state is even there in the first place. And when there's something you don't understand, I think that that means we're not done yet, that more work needs to be done.”
The researchers hope to unravel the lingering mysteries and explore other research avenues their experiments have opened. They are working on additional research to further explore the behaviors of spins in the ferromagnet layer. And, based on their results, they are also optimistic that with further work similar devices may provide a window into the interactions of light and the magnetic excitations in a material—an emerging research field called magnonics.
“I actually think that the most important thing and our most important job as researchers is to look for what you didn't expect because I think that's where the new research and the new physics lies,” says Bøttcher. “So, I am always very excited when I see something I didn't expect, and I think this project was exactly that.”
Original story by Bailey Bedford: https://jqi.umd.edu/news/repurposing-qubit-tech-explore-exotic-superconductivity
In addition to Grankin, Galitski, Bøttcher and Poniatowski, co-authors of the paper include Harvard physics professor Amir Yacoby, Harvard postdoctoral fellow Uri Vool, and Harvard graduate students Zihan Yan and Marie Wesson.
This research was supported by the Quantum Science Center, a National Quantum Information Science Research Center of the US Department of Energy; the NSF NNIN award ECS-00335765; the Department of Defense through the NDSEG fellowship program; the National Science Foundation Grant No. DMR-2037158 and DMR-1708688; the US Army Research Office Contract No. W911NF1310172; the Simons Foundation; and the Gordon and Betty Moore Foundation Grant No. GBMF 9468.
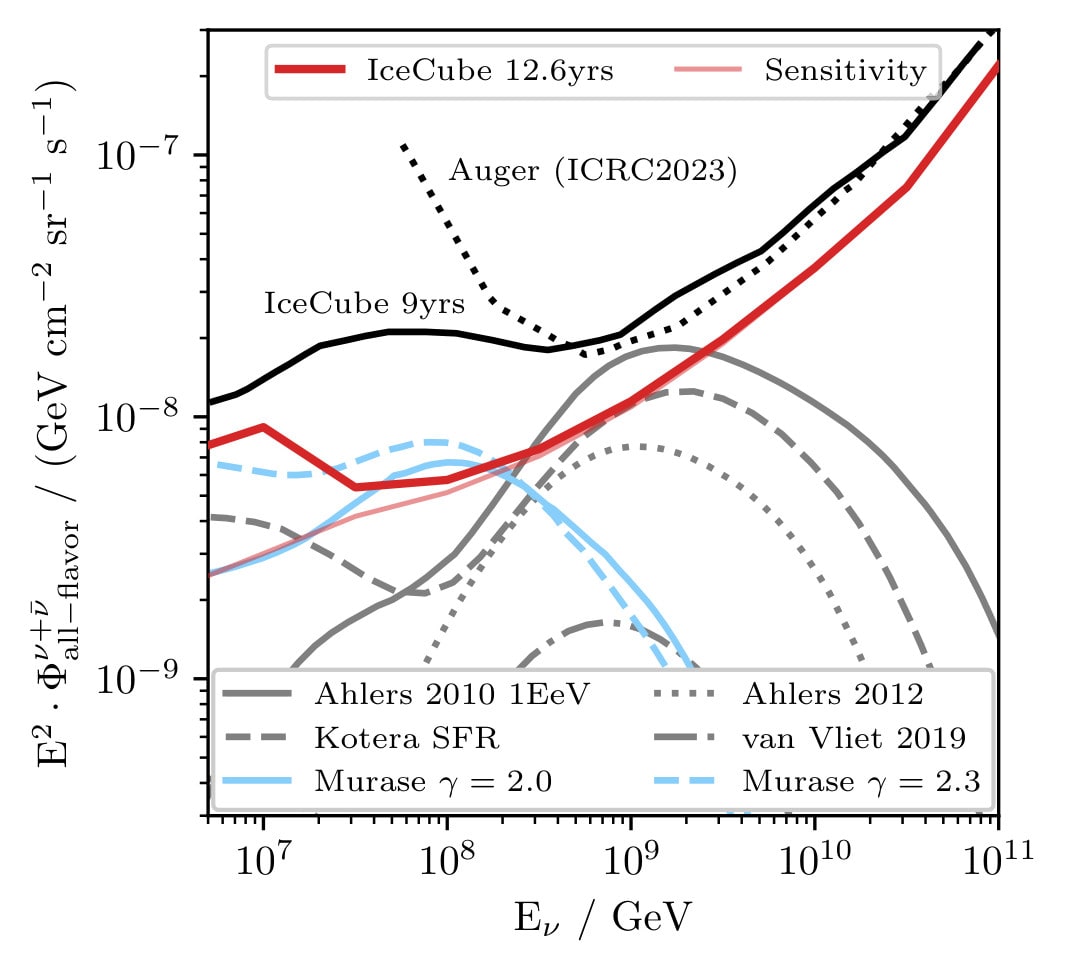 This figure shows the neutrino landscape at the highest energies between a few PeV and 100 EeV (1020 eV). The red line shows the flux limit we set due to not observing any neutrinos with extremely high energies. It is compared to the previous IceCube result using 9 years of data and to a measurement made by the Auger collaboration. Models of the extremely high-energy neutrino flux are shown in grey (cosmogenic neutrinos) and light blue (neutrinos from AGN), which we can also constrain with our analysis. Credit: IceCube CollaborationIn the search for EHE neutrinos, researchers looked for neutrino “events” where neutrinos deposited a huge amount of light inside the detector. However, because most high-energy neutrinos are absorbed by the Earth, the focus of the study shifted to neutrinos arriving sideways at (horizontal) or above (downgoing) IceCube. Focusing on horizontal events in particular also allowed the researchers to eliminate most of the overwhelming background of atmospheric muons caused by cosmic-ray interactions above IceCube in the atmosphere.
This figure shows the neutrino landscape at the highest energies between a few PeV and 100 EeV (1020 eV). The red line shows the flux limit we set due to not observing any neutrinos with extremely high energies. It is compared to the previous IceCube result using 9 years of data and to a measurement made by the Auger collaboration. Models of the extremely high-energy neutrino flux are shown in grey (cosmogenic neutrinos) and light blue (neutrinos from AGN), which we can also constrain with our analysis. Credit: IceCube CollaborationIn the search for EHE neutrinos, researchers looked for neutrino “events” where neutrinos deposited a huge amount of light inside the detector. However, because most high-energy neutrinos are absorbed by the Earth, the focus of the study shifted to neutrinos arriving sideways at (horizontal) or above (downgoing) IceCube. Focusing on horizontal events in particular also allowed the researchers to eliminate most of the overwhelming background of atmospheric muons caused by cosmic-ray interactions above IceCube in the atmosphere. Brian Clark
Brian Clark Maximilian Meier
Maximilian Meier