One of the most exciting applications of quantum computers will be to direct their gaze inwards, at the very quantum rules that make them tick. Quantum computers can be used to simulate quantum physics itself, and perhaps even explore realms that don’t exist anywhere in nature.
But even in the absence of a fully functional, large-scale quantum computer, physicists can use a quantum system they can easily control to emulate a more complicated or less accessible one. Ultracold atoms—atoms that are cooled to temperatures just a tad above absolute zero—are a leading platform for quantum simulation. These atoms can be controlled with laser beams and magnetic fields and coaxed into performing a quantum dance routine choreographed by an experimenter. And it’s also straightforward to peer into their quantum nature using high-resolution imaging to extract information after—or while—they complete their steps.
Now, researchers at the Joint Quantum Institute (JQI) and the NSF Quantum Leap Challenge Institute for Robust Quantum Simulation (RQS), led by former JQI postdoctoral fellow Mingwu Lu and graduate student Graham Reid, have coached their ultracold atoms to do a new dance, adding to the growing toolkit of quantum simulation. In a pair of studies, they’ve bent their atoms out of shape, winding their quantum mechanical spins around in both space and time before tying them off to create a kind of space-time quantum pretzel.
They mapped out the curvy space-time shape they created and reported their results in the journal Physical Review Letters last summer. In a follow-up experiment, they watched as their atoms transitioned between different winding shapes and found a rich structure inaccessible to simple, stationary atoms. They published this result in Physical Review Letters in September.
The windings they studied are related to the mathematical field of topology—the classification of objects according to the number of holes they have. Donuts are topologically identical to hula hoops and coffee mugs since they each have one through-hole. But donuts are distinct from eyeglass frames, which have two holes, or pretzels, which have three.
This deceptively simple classification of shapes has been surprisingly impactful in physics. It has explained things like the quantum Hall effect, which produces a precisely repeatable electrical resistance used to define the resistance standard, and topological insulators, which may one day serve as components of robust quantum computers.

Most solids are crystals, made up of a regular grid extending every which way in a repeating pattern of equally spaced atoms. For free-floating electrons inside this grid, hopping over from one atom to another identical one makes no difference—the landscape is exactly the same as far as the eye can see. A similar grid pops up in the landscape of electron speeds—things may change as the electron starts accelerating, but at certain speeds, the landscape will look the same as if it wasn’t moving at all.
But position and velocity are only two properties of the electron. Another is spin. Spin can behave somewhat independently as position and velocity change, but when the position is shifted by one site or velocity is shifted by one velocity “site,” the spin must remain unchanged—another reflection of the symmetry present in the crystal. But in between two sites or two velocity “sites” anything goes. The winding shape that the spin draws out before coming back to where it started is what defines the topology.
In the world of quantum simulation, ultracold atoms can emulate electrons in a crystal. The role of the crystal is played by lasers, creating a repeating pattern of light for the ultracold atoms to inhabit. The atoms’ location and speed similarly acquire a repeating pattern, and the atomic spins trace out shapes that define the topology.
In their winding experiment, Lu and his labmates devised a two-dimensional crystal, but not in the usual two dimensions of a sheet of paper. One of the dimensions was in space, like the direction along a thin thread, while the other was time. In this sheet composed of space and time, the spin of their atoms drew out a curious shape as a function of the atoms’ velocity in the time-space crystal.
“Topology is defined on surfaces,” says JQI Fellow Ian Spielman, the principal investigator on the research and the associate director for research at RQS . “One of the dimensions defining the surface can be time. This has been known for a while theoretically but is only now being tested experimentally.”
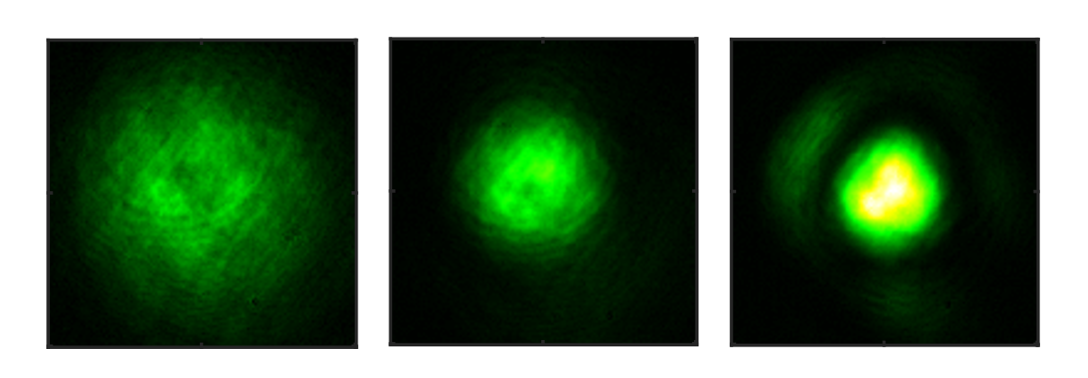
To create a surface that winds in both space and time, the researchers shined lasers from two directions and a radio-frequency magnetic field from above onto their cloud of ultracold atoms. The lasers and magnetic field combine to create areas of higher and lower energy that atoms are pushed away from or drawn towards, like an egg carton for the atoms to live inside of. This carton had a peculiar shape: instead of two rows of slots like in a regular dozen you’d find in a grocery store, there was only one row. And each slot of the carton was made up of two sub-slots (see picture below). This gave the repeating crystal-like pattern along a line in space.
By adjusting how the lasers and magnetic fields align with each other, the team could shift the whole pattern over to the side by one sub-slot (see picture). But they didn’t just swi Two laser configurations that the researchers switched between rhythmically to wind their atoms through space and time (Credit: Mingwu Lu/JQI).tch it once. They rhythmically shook the egg carton back and forth between the two. This rhythmic shaking created a repeating pattern in time, akin to the repeating spatial pattern of nuclei in a crystal.
Two laser configurations that the researchers switched between rhythmically to wind their atoms through space and time (Credit: Mingwu Lu/JQI).tch it once. They rhythmically shook the egg carton back and forth between the two. This rhythmic shaking created a repeating pattern in time, akin to the repeating spatial pattern of nuclei in a crystal.
To do this, they had to make sure their laser egg-carton, as well as the timing of the strobe, were just right. “The hardest part was just getting the timing right,” says Graham Reid, a graduate student in physics and one of the authors on the work. “This experiment really relies on very precise timing of things that you don't know a priori, so you just have to do a lot of tuning.”
After a lot of fine-tuning, however, they experimentally imaged the spin of the atoms in this time-space crystal. They mapped out the winding of the spin as it traversed both time and space on its way back to where it started. This way, they directly measure the winding topology they’d constructed.
Following up on this work, they used the same laser pattern to do a very different topology-related experiment. Instead of looking at a topology in space and time, they focused on just the spatial dimension. This time, they prepared their atoms in different ways: all spin down, all spin up, or a mix.
These weren’t natural, comfortable states for the atoms in the laser pattern they created, and, eventually, the atoms would settle to their more natural states—their equilibrium states. But along the way, they could capture freeze frames of several different topological shapes—some that would never occur but for an instant. These results have revealed new mysteries that the researchers are eager to investigate.
“There are two big questions that I think would be great to answer,” Spielman says. “The first is that the space and time topology result really only worked at a fine-tuned timing. I wonder if there is a way to make that robust. Second, for out-of-equilibrium topology, I am interested to see what happens when we quickly switch between a wider variety of topological states.”
Original story by Dina Genkina: https://jqi.umd.edu/news/twisting-atoms-through-space-and-time
In addition to Spielman, who is also a fellow at the National Institute of Standards and Technology, Reid, and Lu, who is now at Atom Computing, authors on the papers included Amilson Fritsch, a former postdoctoral fellow at JQI now at the University of Sao Paulo Sao Carlos, and Alina Piñeiro, a graduate student in physics at JQI.