Our world only exists thanks to the diverse properties of the many materials that make it up. The differences between all those materials result from more than just which atoms and molecules form them. A material’s properties also depend on how those basic building blocks are organized in space. For instance, the only difference between a hard diamond and the flaky graphite in pencils is the pattern that carbon atoms form in the material.
Studying the repeating structures of materials has been instrumental to the field of materials science for the past century. But since 2012, researchers have branched out and started investigating a new type of material in which the basic building blocks order themselves into a stable structure that repeats in time.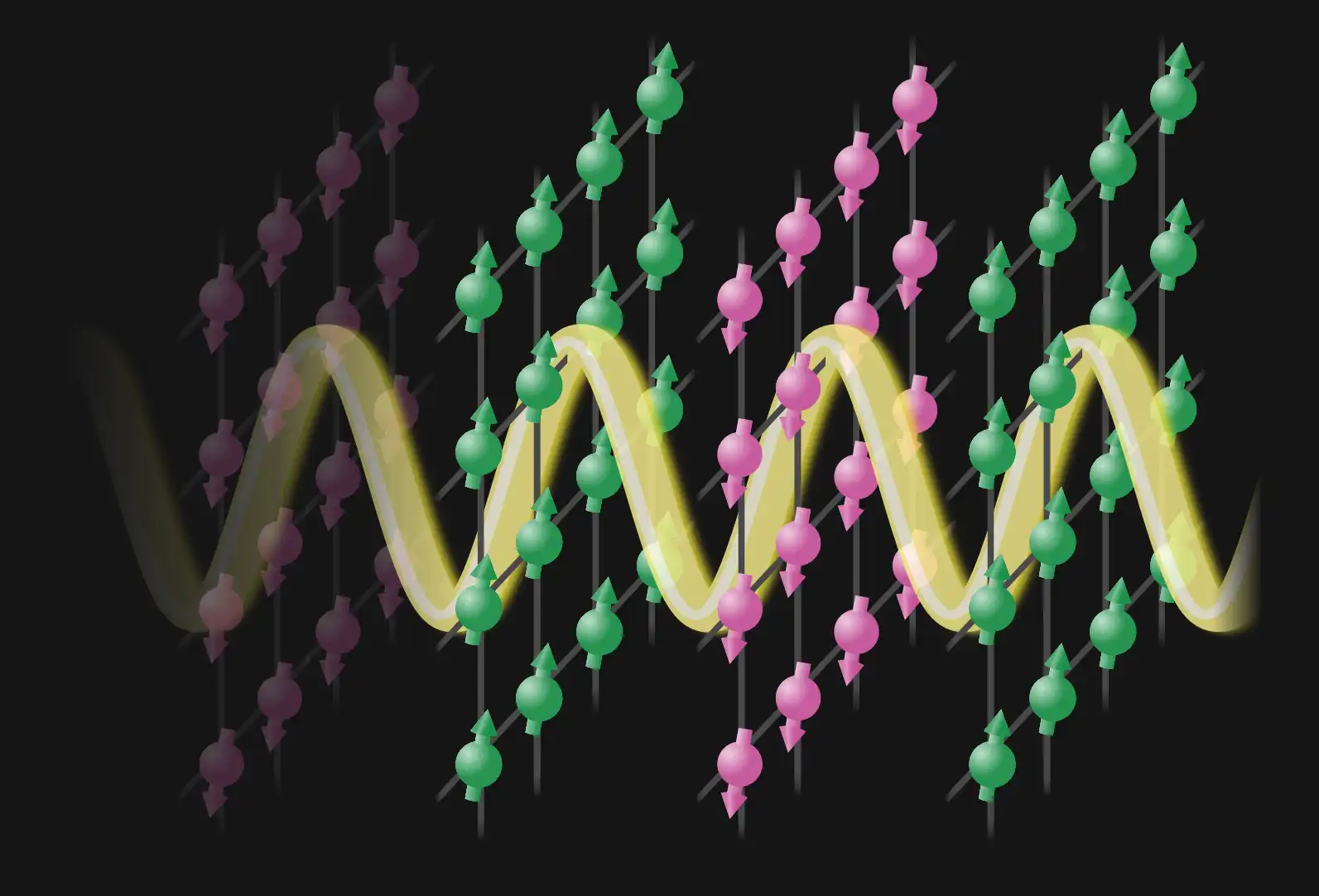
The pink and green sheets of arrows represent a 2D material in two different states. As time progresses from left to right, the material oscillates between each state, forming a time crystal. The states flip back and forth at half the rate of the force driving them, which is represented by the yellow wave. (Credit: Stuart Yi-Thomas, UMD)
These special materials are called “time crystals.” (Whether or not a structure makes a pretty jewel, physicists call all solid, orderly structures of repeating atoms or molecules crystals.) Time crystals are collections of particles that undergo repetitive patterns in time, and they can only exist when there is an external force supplying energy to them. But not everything driven into a periodic pattern is a time crystal.
To be a time crystal, the repeating pattern must arise from the interactions of the constituent particles and not just mirror the periodic pattern of the driving force. Additionally, a time crystal’s structure provides stability so that it can maintain its pattern even when the driving force temporarily falters or the time crystal is nudged by another force. (So the pistons of a car engine making the car’s wheels rotate in unison as it drives down the road isn’t an example of a time crystal.)
Researchers have been able to create time crystals in the lab and describe their observed behaviors. However, descriptions of time crystals have generally focused on a particular experimental result and haven’t delved into the theory of what fundamentally makes them form. The lack of a robust theoretical framework leaves many open questions in the field and gives researchers little guidance on which ingredients are useful for creating new time crystals.
In an article published late last year in the journal Physical Review Letters, JQI graduate student Stuart Yi-Thomas and Professor and JQI co-Director Jay Sau presented a new framework for studying time crystals formed from specific ingredients. They made their framework by adapting a widely used and versatile theory for describing phases of matter in quantum systems.
To a physicist, phases of matter refer to more than just solids, liquids and gases and include other organizations of matter such as plasmas, magnets and superfluids. Phases represent distinctive states that a material can be in. When a condition like the temperature, pressure or magnetic field strength varies, a material can switch between phases—undergo a phase transition—and suddenly behave dramatically differently, like water freezing into ice or aluminum becoming superconducting when cooled in liquid helium.
“Time crystals constitute a new phase of matter, which has garnered a lot of excitement in the past decade or so,” says Yi-Thomas who is also a graduate student of the Condensed Matter Theory Center (CMTC). “And heretofore, it has not really been understood as other phases of matter have.”
The framework that Sau and Yi-Thomas crafted allows researchers to study time crystals more like traditional phases and provides insights into when time crystals will form and when they will fall apart.
Some researchers hope that as time crystals become better understood their stability will be put to work as memory in quantum computers.
“The way we use materials and technology is mostly centered around the phases they are in,” says Sau, who is also a member of CMTC. “Solids, liquids, gases, superconductors, metals, insulators and magnets—these are all examples of phases of matter, and their properties are what we use to build technology. So the hope is that once we have other, newer phases we should be able to find technological applications for them.”
To study time crystals as a phase of matter, Sau and Yi-Thomas chose not to focus on an individual time crystal experiment. Instead, they stayed very general and picked out a few well-understood ingredients they thought were promising candidates for forming a time crystal.
The critical ingredient they needed to identify was a type of basic building block that could come together and produce the pattern. The pair focused their investigation on building blocks that all interact with each other and that each is what physicists call an “oscillator,” which means it behaves like a spring or pendulum that can bounce or swing between different states. But Sau and Yi-Thomas didn’t think just any oscillator would work; they wanted a particular type of oscillator—called a non-linear oscillator—that changes how strongly it responds when pushed far enough away from its resting state. There are many types of nonlinear oscillators from car shock springs to microscopic carbon nanotubes to electrical effects in circuits, and Sau and Yi-Thomas didn’t want to specify what sort of non-linear oscillator if they didn’t have to.
Another crucial ingredient to select was an energy input to drive the oscillators back and forth between states. The pair focused on an energy source that would create a phenomenon called “parametric amplification” in a collection of oscillators. Parametric amplification produces oscillating behaviors that reminded them of the repetition of a time crystal, but it comes with an amplification of the oscillations as energy is fed in over time. To get parametric amplification, the frequency of the driving must be selected based on the properties of the oscillators being used.
Then they needed an ingredient to balance the steady increase in energy. So they identified a third simple—but likely necessary—ingredient: friction or some other interaction that can bleed off energy and let the pieces settle into a stable pattern.
Together, these three requirements translate into the constituents of the time crystal needing to be what physicists categorize as “weakly-nonlinear parametrically-driven dissipative coupled oscillators.”
“It sounds very specific because there's a lot of qualifiers, but for this specific model, it's kind of the simplest model we could do,” Yi-Thomas says. “And we expect that similar results would apply to a wide variety of systems.”
Despite all the demands, several common experimental setups, including certain laser setups and specialized electrical circuits, can check all the identified boxes and thus provide a suitable place to try to make or model new time crystals.
Without worrying about which experimental setup might be used, Sau and Yi-Thomas needed a way to analyze if there are conditions under which their ingredients produce a time crystal. Since they wanted to put time crystals on a similar footing as more traditional phases, they turned to a classic tool for studying phases of matter in quantum systems. That tool, called the Ginzburg-Landau theory, was created to describe superconductivity and the phase transition associated with a material becoming or ceasing to be a superconductor. Over time, physicists have used the same basic math to describe other phases like magnets and Bose-Einstein condensates as well.
The pair adapted the existing theory’s descriptions of phase transitions to apply to the traits they had identified. The resulting framework suggested that experiments with the identified ingredients should be able to form a time crystal.
“To use an idiom, we show that you can build a time crystal with things you can find around the house,” Yi-Thomas says. “You don't need a complex cellular automaton. You don't need many-body localization, or these exotic things. Just with these ubiquitous elements, you can still create a symmetry-breaking phase—a time crystal.”
The paper didn’t argue that using these ingredients is the only way to produce a time crystal but instead highlighted them as promising (and convenient) candidates for researchers to consider.
In the paper, Sau and Yi-Thomas discussed what their new framework revealed about the conditions under which a time crystal should form or break down. They found that the oscillators need to respond with a certain amount of randomness—noise. Just the right amount of noise helps a time crystal lose energy and achieve stability. If there isn’t enough randomness, the steady input of energy tends to introduce too much chaos and make the pieces shift around unpredictably. If instead there is too much randomness in the noise, the randomness itself prevents a stable pattern from emerging. The pair’s calculations suggest a range of possible noise levels that supply an appropriate amount of randomness to form a time crystal.
The pair also tackled the question of whether the stability of a time crystal improves with the number of particles in it, similar to the way normal phases are more stable in larger systems. For instance, the larger a magnet is, the more improbable it will demagnetize or reverse its polarity.
Time crystals might also have an intrinsic stability that increases with size, but many researchers suspect that as experiments increase in size larger time crystals will continue to quickly fall out of their coordinated dances. So Sau and Yi-Thomas looked at larger and larger models of time crystals in their framework to predict whether the crucial stability is doomed to fail or might actually be robust. Their calculations predicted that as time crystals grow, they will experience an increase in stability, similar to magnets and other phases.
Now the framework is available as a tool for researchers investigating a diverse pool of time crystal experiments. Since the theory lays out specific traits that it predicts can create a time crystal, it provides a guide for selecting experiments and conditions that might be fruitful for researchers searching for new time crystals. It also provides a way to predict and study both the conditions under which time crystals fail and when they might experience a shift to a slightly new pattern in time.
Sau and Yi-Thomas hope that other researchers will apply their framework to new time crystal experiments and that research on the time crystal phase of matter will eventually be as robust as research into other phases.
Original story by Bailey Bedford: https://jqi.umd.edu/news/time-crystal-research-enters-new-phase